
★実数に於いて、数は変化することが不可能であることの証明。
ある事象に於いて、その事象の元が、変化することが可能である事の条件を
3つ挙げる。
①ある事象が、事象を構成する元の集合であるとみなせる、元を持っている。
②その集合に於いて、元をある基準で整列させることが可能であるか、又は
その事象の元は、元々整列した状態で存在しているとみなせる。
③整列した状態で、任意の元と、任意の元に最も近い隣の元の、両方の元の
実在が自明であるか、またはその実在を証明することが出来る。
ある事象が、この3つの条件を全て満たす時に、その事象に於いて、元は変化
することが可能であると定義する。
ここで実数に於いて、数が変化することが可能か否かを、上記の条件と照らし
合せて考察する。
実数は数を元とする無限集合とみなせる。
かつ、実数の元である数は、元々大小順に稠密に整列しているとみなせる。
よってここで、ある数と、それに最も近い隣の数の、両方の実在が自明である
か、またはその実在を証明できるのであれば、実数に於いて数は、変化する
ことが可能であることを、証明できたことになる。
ここで実数中の数1と、1に最も近い隣の数が、実在するか否かを、デデキント
切断を用いて考察する。
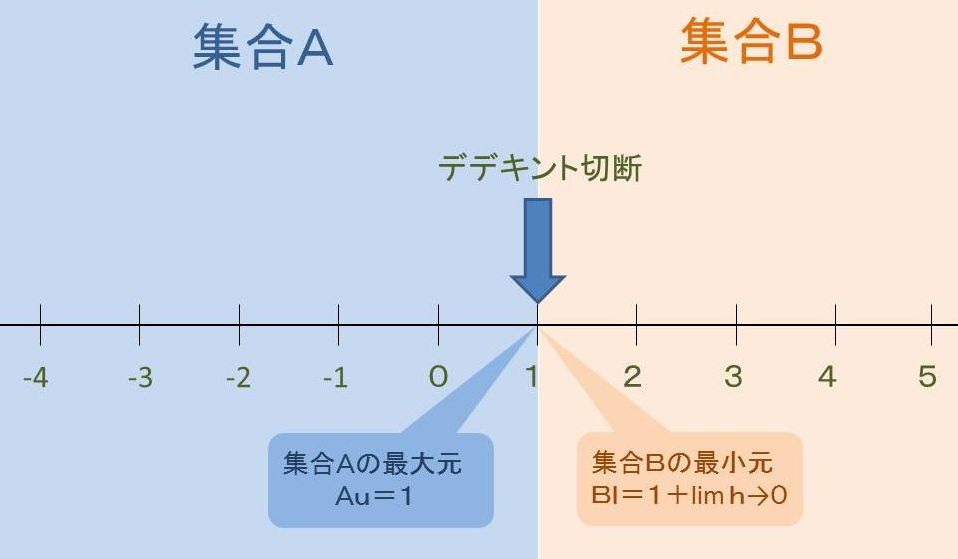
実数の集合Rを数1に於いてデデキント切断し、数1を下組に含めた集合Aと
上組の集合Bの2つの集合とに分けて考える。
集合Aの最大元は、最大元をAuとおくと、Au=1である。集合Bの最小元を求
める式は、最小元をBlとおくと、Bl=1+lim h→0と定義できる。
lim h→0は実数の定義により、どこまでも無限に0に近づくことができるため
最小元Blは、特定することができないことが分かる。
ここで最小元Blが、集合B中に実在すると仮定する。
最小元Blが、集合B中に実在する場合、Blは集合B中の、1つの元なので、
無限集合である集合B中には、必ず最小元Blよりも、更に1に近い最小元が
存在する結果となる。
このように最小元Blは、Blが集合B中に実在した瞬間に、最小元でなくなる。
このことは、次の事実を示している。
最小元Blは、たとえそれが集合B中に、一つの元としてに存在すると、予測さ
れるとしても、実際に最小元として、集合B中に実在することが許されない。
以上より、最小元Blは、集合B中には、実在し得ないことが分かる。
実数に於いて数1の実在は自明である。しかし数1に最も近い隣の数の実在
は否定される。このことは実数の集合Rの、全てのデデキント切断点に於いて
同様であると考えられる。以上から、
実数に於いて、数は変化することが不可能であることが証明される。
★実数は非可算である。
数学での数の変化の基本は、加減算である。つまり、実数に於いて、数が変化
することが不可能であるとは、実数に於いて、加減算が成り立たない事と同じ
事を意味する。
実際に数学においては、実数は非可算であることが既に証明されている。
ここで独自に、デデキント切断を用いて、実数は非可算であることを証明する。
常識では、実数に於いても0+1=1は必ず成り立つと誰もが考える。
そこで、この計算について、詳しく調べてみる。
0+1=1の意味は、実数を数直線と考えた場合、数0に、長さ1の直線を足し
た場合、その端は数1と同じ位置になる。という意味を持っている。
数0と数1は実数に於いて、実在する数と考えられる。しかし問題となるのは、
実数に於ける長さ1の直線の大きさ(長さ)である。
実数に於いて、長さ1の直線の大きさを求めるには、数0 と数1 でデデキント
切断し、その差を求める必要がある。そしてデデキント切断では、切断点をどち
らに含めるか、決定する必要があるので、式の一方に必ず lim h→x を含まな
ければならない。
つまり実数に於ける長さ1の直線の大きさは
1-(lim h→0) 又は (lim h→1)-0 のどちらかとなる。
lim h→x は実数の定義によりどこまでも無限に対象xの数に近づけるので、
実数に於いての、長さ1の直線の大きさは、特定出来ないことになる。
稠密な実数に於いて0+1=1は
0+(1-(lim h→0))=1 又は 0+((lim h→1)-0)=1 と書き換えられる。
ここで、実数の定義により lim h→0 、 lim h→1 は特定できない。
以上より、実数において0+1=1は厳密には成り立たないことが証明される。
★数の変化は、離散的に変化する整数に於いてのみ可能であることの証明。
実数に於いて、数が変化することが不可能である事の、根本理由は、実数では
数が隙間なく稠密に存在する為、任意の数xでデデキント切断した場合に、xとx
に最も近い隣の数の、どちらか一方の、実在を証明できなくなる事による。
ところが、整数では数の変化が離散的であるために、任意の数xで、デデキント
切断しても、xとxに最も近い隣の数の実在が、両方共に自明となる。
以上から、数の変化は、離散的に変化する、整数に於いてのみ、可能であること
が証明される。
そして、この証明から、数学に於ける数の変化について、次の原則が成立つこ
とが導かれる。
「ある集合に於いて、集合中の元が、変化可能であるためには、元が集合中に
離散して存在する必要がある」
短い表現にすると
「変化は離散的にしか起こり得ない」
となる。
★離散的変化の定義。
<大雑把な定義>
不連続な変化。変化は一瞬で起こるので、変化の過程を分析できない。
<詳細な定義>
変化の最小単位に、それ以上は分割不可能な単位を持つ変化のことを指す。
その変化は変位0間に一瞬で起こり、変化の過程を観察したり、分析したり
することは原理的に不可能である。しかし変化後の結果を調べたり認識する
ことは可能である。
★数学上だけの変化の原則から、数学で記述され得る、全ての事象に於ける
変化の原則への拡張。
数学に於いて、数の変化が離散的にしか起こり得ないのであれば、数学を用い
て記述され得る、全ての事象中の変化に於いて、その変化は、離散的である事
が推察される。
このことから、数学を用いて記述され得る、全ての事象中の変化に於いて、次
の原則が成り立つと推察される。
「変化は離散的にしか起こり得ない」
例えば物理学に於ける時間でさえも、その変化は離散的であることが推察され
時間の変化によって定義される空間も、離散的構造を持つことが推察される。
そして空間が離散的構造を持つのであれば、ゼノンのパラドックスは、物理空間
に於いては生じない。
★「変化は離散的にしか起こり得ない」の原則の物理学での有効性。
数学に於いての数の変化の原則から、数学で記述され得る、全ての事象中の
変化に於いて次の原則が成立つことを推察した。
「変化は離散的にしか起こり得ない」
この原則が、物理学の「場の量子論」に於いて、有効であるか否か考察する。
場の量子論では、場の量の期待値は主に経路積分を用いて計算される。
この時、時空が連続であるとの前提で、経路積分の計算を行うと、計算過程に
於いて無限大の発散が生じ、計算を続行できないという問題が発生する。
そこで無限大の発散を回避する為に、摂動展開とくりこみを用いて計算するので
あるが、摂動展開では実験結果と計算結果があまり合わなかったり、くりこみが
不可能な事象の場合もある。
そこで時空を連続ではなく、分割不可能な最小単位をもつ格子状と仮定した理論
である「格子上の場の理論」を使用して計算する。
すると計算途中で無限大に発散することもなく、また計算結果の精度も上がる。
「変化は離散的にしか起こり得ない」の原則に従えば、時間でさえも離散的にしか
変化出来ず、その結果時空は、離散的構造を持つと予測される。
場の量子論に於いて、「格子上の場の理論」による計算が非常に有効であるのは
「変化は離散的にしか起こり得ない」の原則から予測されるように、実際の時空が
離散的構造をもっているからであると考えられる。
●● 謝辞 ●●
ここに於いて、この証明を、最後まで完了することができたのは、自分だけの発想
によるものではありません。当初は直感による「変化は離散的にしか起こり得ない」
との考えしか思い浮かびませんでした。もしそこに、デデキント切断のことを教えてく
ださった、うつぎ氏の適切なアドバイスがなければ、証明を理論的に完了することが
できなかったと思います。
うつぎ氏の数理物理に関する深く・的確な洞察力とそのアドバイスに感謝します。
うつぎ氏のHPへのLink
copyright©2017 量子力学現象の新解釈 all rights reserved.